Tutorial
Click here to download the PDF of the problems or click here to see the challenge results.
Contents:
- Problem A: The Tallest One
- Problem B: Behind The Tallest One
- Problem C: The Best Three
- Problem D: The Swaps
- Problem E: Mike’s Puzzle 2.0
Problem A: The Tallest One
This problem requires a typical tracking of an optimum value (e.g. maximum or minimum) within a list. Generally, finding the maximum/minimum number from a given list involves visiting each number and remember the biggest/smallest you have encountered so far. This works for both sorted and unsorted lists.
For a sorted lists, the minimum and maximum can quickly be determined from the first and last items (depending on whether the list is sorted in descending or ascending order).
Given N numbers (heights in this case), we can maintain two variables: height that will temporarily store the value of each student’s height (one at a time), and maxHeight that will store the height of the tallest student found so far. At first, we can initialize maxHeight with the least possible height (i.e. zero). Note that zero or any negative number will work.
Then, repeating N times, we can input the next height and compare it with maxHeight. If it is greater, we will update maxHeight to be the value of this height. After comparing all N heights, maxHeight will have the tallest student’s height. This can be implemented as follows in C++.
// Get the count of total students
int N;
cin >> N;
// Find the tallest height
int height, maxHeight = 0;
for( int i = 0; i < N; i++ ){
// Get the height of next student
cin >> height;
// Check if this height is taller than the current tallest
if( height > maxHeight ) maxHeight = height;
}
// Display the tallest height
cout << maxHeight << endl;Code language: JavaScript (javascript)Notice that we did not store all the numbers before finding the tallest height. This is because we do not need to remember all the heights, only the tallest height seen so far.
Problem B: Behind The Tallest One
Since the problem guarantees that there is only a single tallest student in the class, we can use the solution for Problem A and calculate the position of the tallest student (position). Then, the number of students behind the tallest students will be “N - position“.
// Get count of total students
int N;
cin >> N;
// Find the tallest
int height, maxHeight = 0, position;
for( int i = 0; i < N; i++ ){
// Get the height of next student
cin >> height;
// Check if this height is taller than the current tallest
if( height > maxHeight ){
maxHeight = height;
position = i + 1;
}
}
// Display the count of students behind the tallest
cout << N - position << endl;Code language: JavaScript (javascript)Similar to Problem A above, we did not store all the numbers before finding the tallest height. This is because we do not need to remember all the heights, only the tallest height seen so far (and its position).
Problem C: The Best Three
The problem involves selecting three adjacent scores at a time and check if they give the best total.
Since we are guaranteed to always have at least three scores, we can maintain an adjustable array (i.e. vector) of the scores. At first, we will add the initial three scores, at once, and assume they give the best total (it is the only triple so far).
Then, we will add one score at a time at the end of the list. After adding each score, we will check if the last three scores give a better total. Once we are done adding all numbers into the list, the best score will have been determined and we can display it.
// Get count of total students
int N;
cin >> N;
vector<int> scores(3); // Stores all scores in the class. At first, has space for the first three
// Get the first three scores
cin >> scores[0] >> scores[1] >> scores[2];
// Assume the first three scores are the better
int maxTriple = scores[0] + scores[1] + scores[2];
int pos = 2;
// Determine if there is a better triple
for( int i = 0; i < N-3; i++ ){
// Add the next score into the list
int score;
cin >> score;
scores.push_back(score);
// Check if the last three scores are the best
int p = scores.size() - 1;
if( scores[p-2] + scores[p-1] + scores[p] > maxTriple ){
maxTriple = scores[p-2] + scores[p-1] + scores[p];
pos = p;
}
}
// Display the best triple
cout << scores[pos-2] << " " << scores[pos-1] << " " << scores[pos] << endl;Code language: JavaScript (javascript)Problem D: The Swaps
This problem at its core is a sorting problem. This is because at the end of the day, we need to make sure that each student stands behind a student who is shorter or the same height. The challenge is to sort the student in the minimum number of swaps possible.
The problem assumes that all students have different heights. Think of how you would modify this solution if students with duplicate heights were allowed.
There are many algorithms for sorting. Each algorithm has its advantages and disadvantages. Furthermore, some algorithms are useful for small lists (e.g. bubble sort, selection sort, and insertion sort) while others are preferable for large lists (e.g. merge sort, and quick sort). We recommend that you understand how to implement the bubble, selection, and insertion sorting algorithms.
Selection sort is the most useful for counting the minimum swaps. Selection sort arranges a list in a sorted order minimizing the number of swaps needed. Refer to this tutorial for a detailed explanation of how a selection sort works. We can implement the algorithm to solve the problem as follows.
// Get count of total students
int N;
cin >> N;
// Get all students heights
int heights[N];
for( int i = 0; i < N; i++ ) cin >> heights[i];
// Compute minimum swaps
int swaps = 0;
for( int range = N-1; range > 0; range-- ){
// Determine the tallest within the current range
int tallestPos = 0;
for( int pos = 1; pos < range; pos++ )
if( heights[pos] > heights[tallestPos] ) tallestPos = pos;
// Move the tallest to the back of the range if he/she is not there
if( heights[tallestPos] > heights[range] ){
swaps++;
int h = heights[range];
heights[range] = heights[tallestPos];
heights[tallestPos] = h;
}
}
cout << swaps << endl;Code language: JavaScript (javascript)Problem E: Mike’s Puzzle 2.0
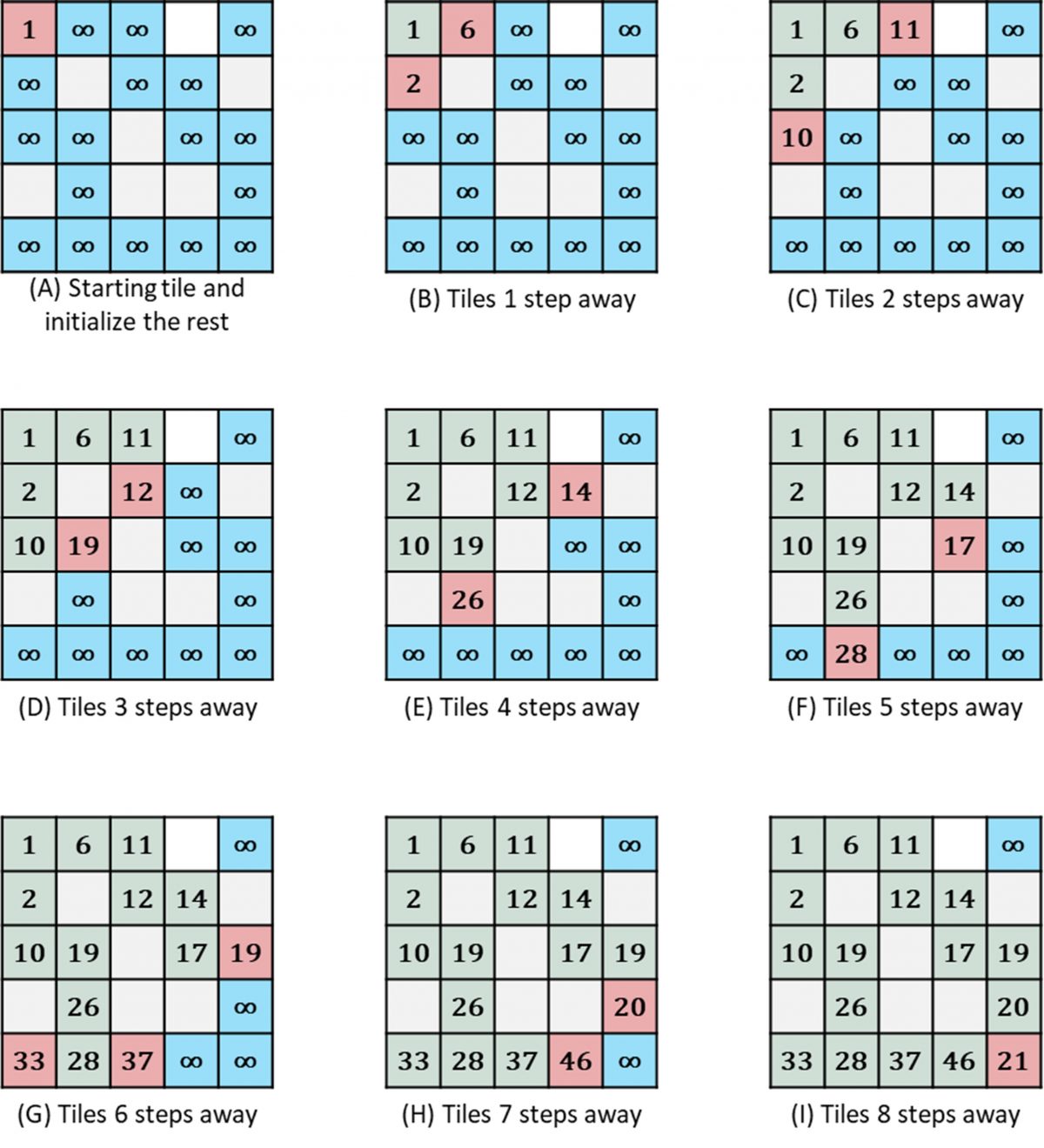
Perhaps a good way to describe an approach to solving this problem is with an example. Suppose we have a grid below.
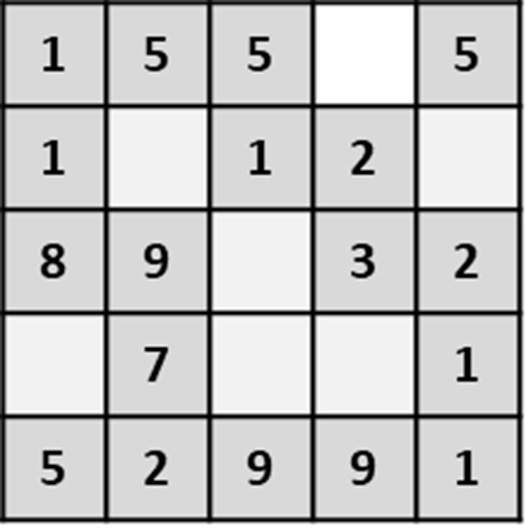
The objective is to find the shortest path that runs from the top left corner (0, 0) to the bottom right corner (4, 4).
Starting with the top left corner, we can calculate the distance of adjacent tiles, one at a time, until we reach the bottom right. Study the steps below.
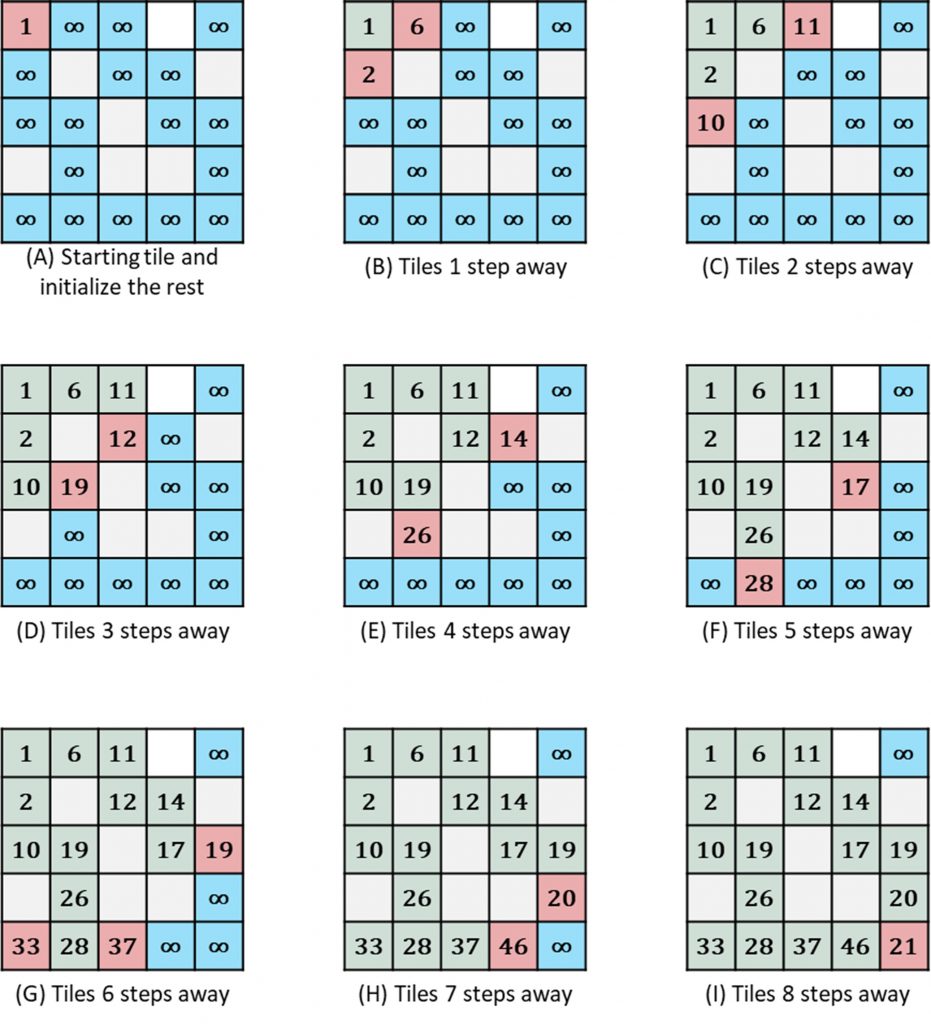
First, we start by assigning the distance of the starting tile (in Step A). Then (in Step B), we calculate the distances of all tiles that are 1 step away from the starting tile (i.e. the tiles that are directly connected to the starting tile). Then (in Step C), we calculate the tiles are 2 steps away, since we already have the distances of all 1 step-away tiles. When there is more than one way to calculate the distance of a tile (e.g. the last tile in Step I), the shorter distance is selected because we are interested with the shortest distance. This continues until all paths have been completed (i.e. all reachable tiles have been visited).
This approach of processing all 1 step away tiles before going to the 2 steps away, and then process the 2 step away tiles before moving to the 3 steps away, and so on, is called breadth first search. This ensures that all correct shortest distances for tiles in step N have been computed before computing the distances of tiles in step N+1.
Technically, this method of calculating the shortest path between two points is called Dijkstra’s Shortest Path First algorithm (or simply Dijkstra’s algorithm).
We can simply implement that above algorithm as follows.
#include<iostream> // cin, cout, endl, pair, min
#include<cstdio> // freopen, stdin, stdout
#include<climits> // INT_MAX
#include<queue> // queue
using namespace std;
int main(){
freopen("1.in", "r", stdin);
//freopen("1.out", "w", stdout);
// Get count of total students
int N;
cin >> N;
// Get the grid
int G[N][N]; // The grid
int D[N][N]; // The distance of each tile from the beginning
bool V[N][N]; // Tracks if a tile has been visited
for( int x = 0; x < N; x++ ){
for( int y = 0; y < N; y++ ){
cin >> G[x][y]; // Get tile's weight
D[x][y] = INT_MAX; // Initialize tile distance
V[x][y] = false; // Initialize tile as not visited
}
}
// Add the starting point into the queue
queue< pair<int, int> > Q; // Tracks reachable tiles that need to be visited
Q.push(make_pair(0, 0));
D[0][0] = G[0][0];
// Compute the distance of all tiles reachable from (0,0)
while( Q.size() > 0 ){
// Remove the next tile from the queue
pair<int, int> p = Q.front(); Q.pop();
int x = p.first, y = p.second;
// Check for a non-visited tile to the right
if( y+1 < N && !V[x][y+1] && G[x][y+1] ){
D[x][y+1] = min(D[x][y] + G[x][y+1], D[x][y+1]);
if( !(x==N-1 && y==N-1) ) Q.push(make_pair(x, y+1));
}
// Check for a non-visited tile to the left
if( y-1 >= 0 && !V[x][y-1] && G[x][y-1] ){
D[x][y-1] = min(D[x][y] + G[x][y-1], D[x][y-1]);
if( x!=N-1 || y!=N-1 ) Q.push(make_pair(x, y-1));
}
// Check for a non-visited tile below
if( x+1 < N && !V[x+1][y] && G[x+1][y] ){
D[x+1][y] = min(D[x][y] + G[x+1][y], D[x+1][y]);
if( x!=N-1 || y!=N-1 ) Q.push(make_pair(x+1, y));
}
// Check for a non-visited tile above
if( x-1 >= 0 && !V[x-1][y] && G[x-1][y]){
D[x-1][y] = min(D[x][y] + G[x-1][y], D[x-1][y]);
if( x!=N-1 || y!=N-1 ) Q.push(make_pair(x-1, y));
}
// Mark the current tile as visited if it is not the destination
if( x != N-1 || y != N-1 ) V[x][y] = true;
}
cout << D[N-1][N-1] << endl;
return 0;
}Code language: PHP (php)